Big O notation

Introduction

Big O notation is a way for computer scientists to measure the complexity of an algorithm. In short, it’s a way to measure the cost of an algorithm and how long it will take to run.

When we’re working with a small amount of data, it doesn’t really matter if our program is efficient or not. What about in the case of a database that has thousands, or maybe even millions, of records? In this case, an inefficient program will take significantly much longer to finish working through the set of records. Big O notation addresses this by determining the time complexity (time to run) for a function to finish.

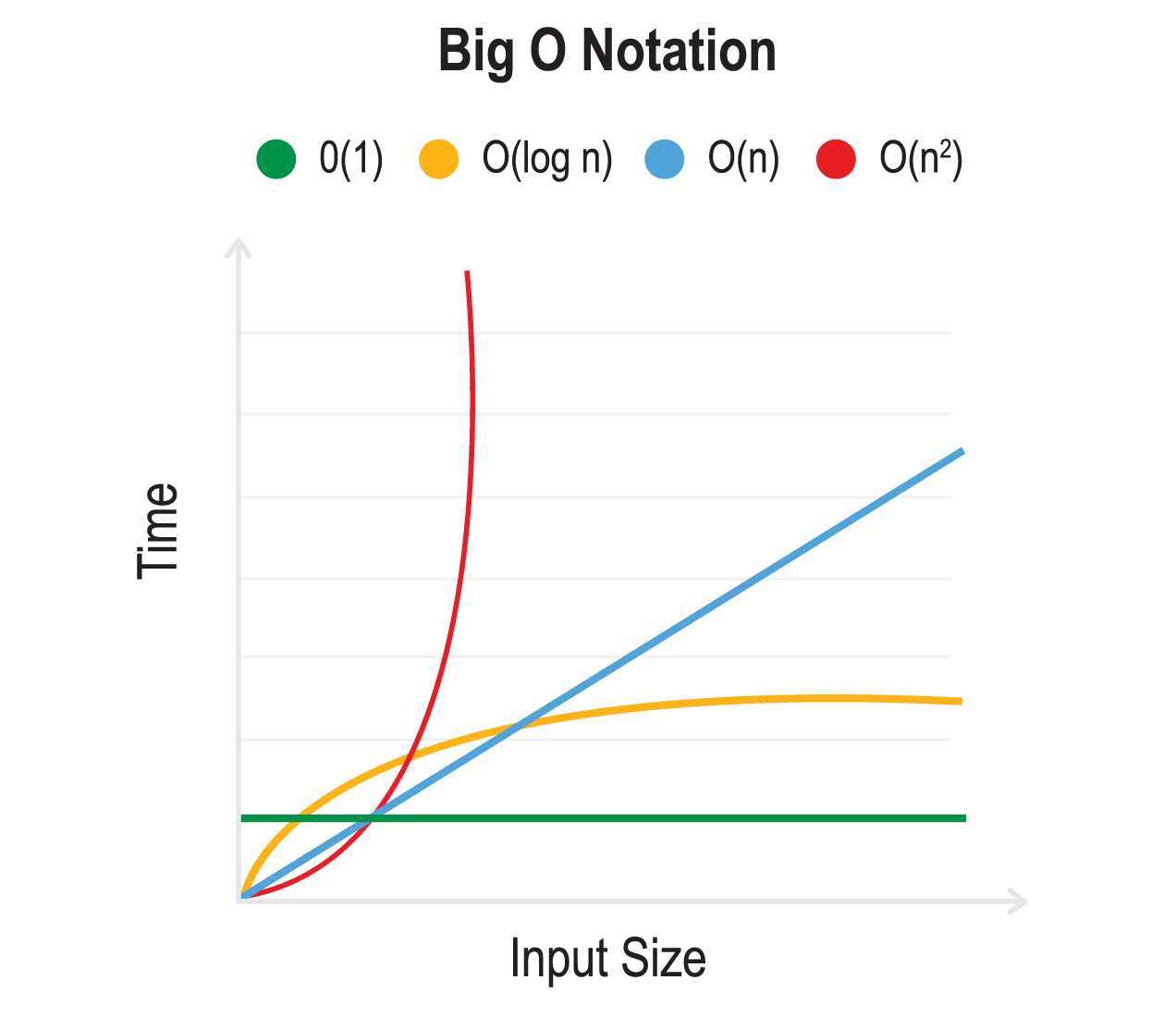
Big O Notation

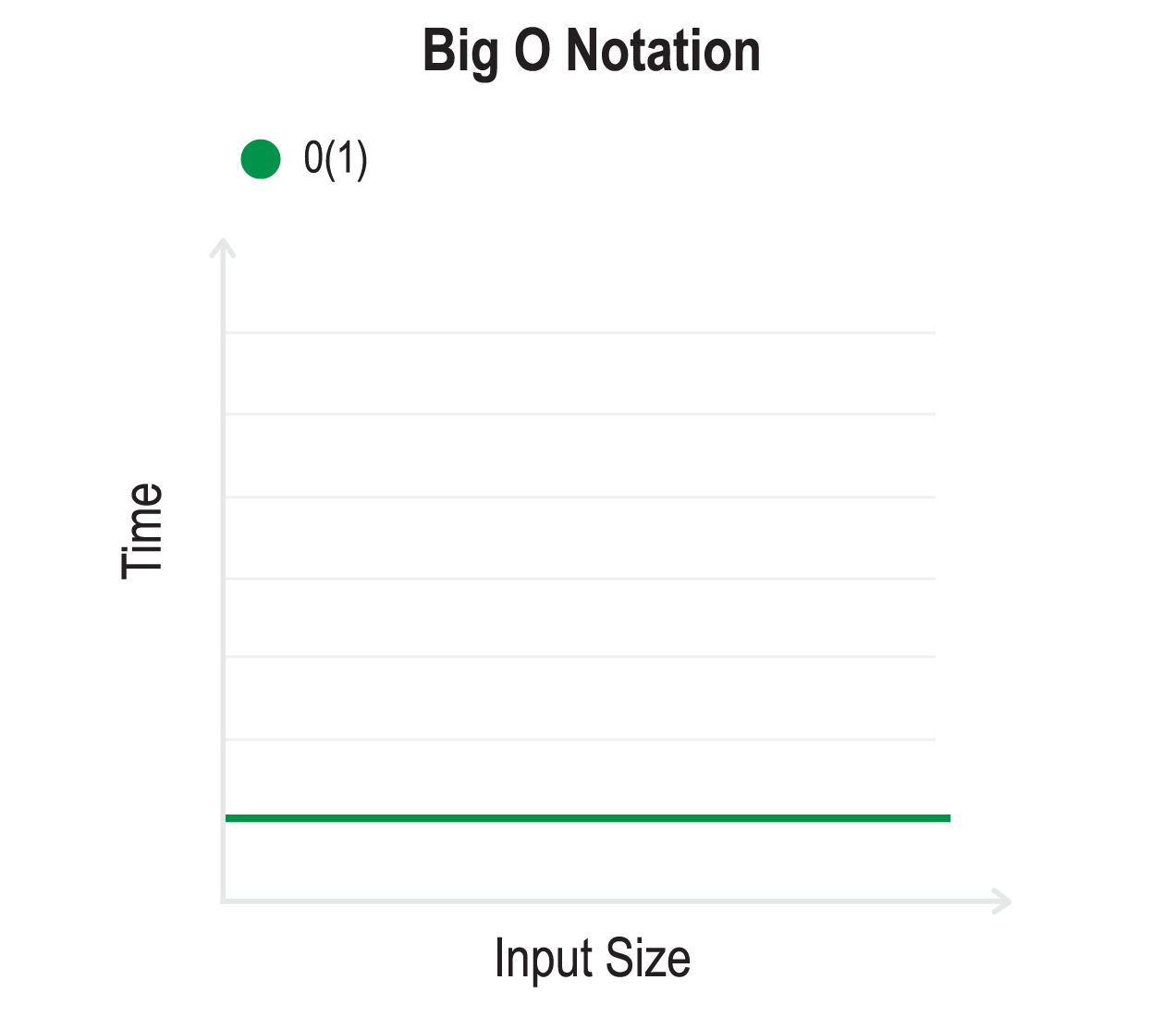
O(1) - Constant time

O(1) means that it takes a constant time to run an algorithm regardless of the input size.

This is when your code can complete in a single step, such as using an array index or object key to find a value.

For example, the following would be in O(1) notation:

const values = [0, 1, 2, 3, 4];

function getValue(index) {
  // This code is O(1) notation as it can immediately
  // access the required value.
  const value = values[index];

  return value;
}

const myValue = getValue(2);

Examples of O(1) notation include:

Accessing properties of an object using a key
Adding and removing items from a stack
Insertion and removal of items from a queue
Math operations

O(1) Constant Time

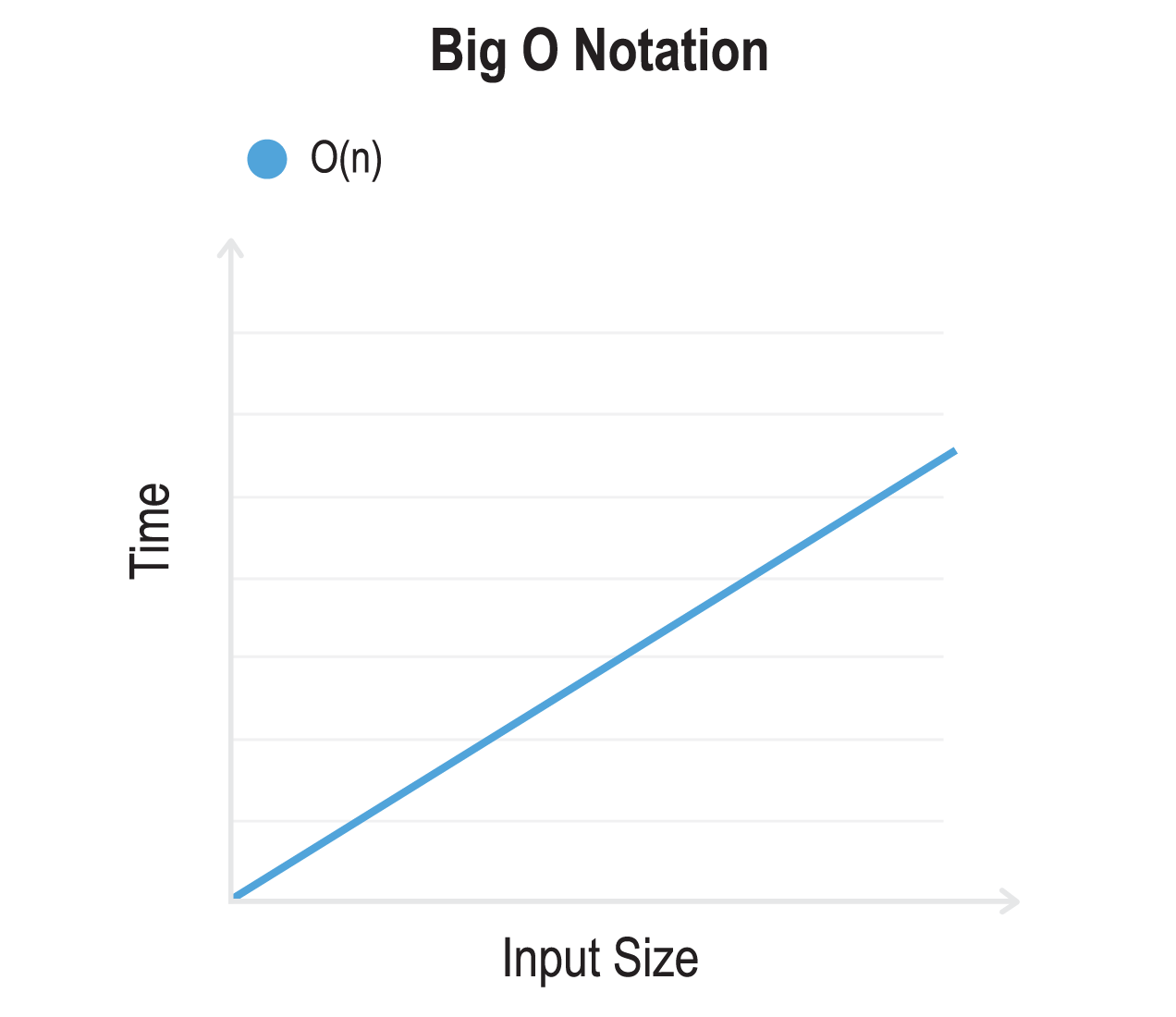
O(n) - Linear time

O(n) means that the run-time increases at the same pace as the input.

This means that our run-time will grow proportionally to the input that we give it.

For example, if it took 1 minute to process a record then if we had 100 records it would take 100 minutes to process all of them (1 x 100 = 100).

Examples of O(n) notation include:

O(n) Linear Time

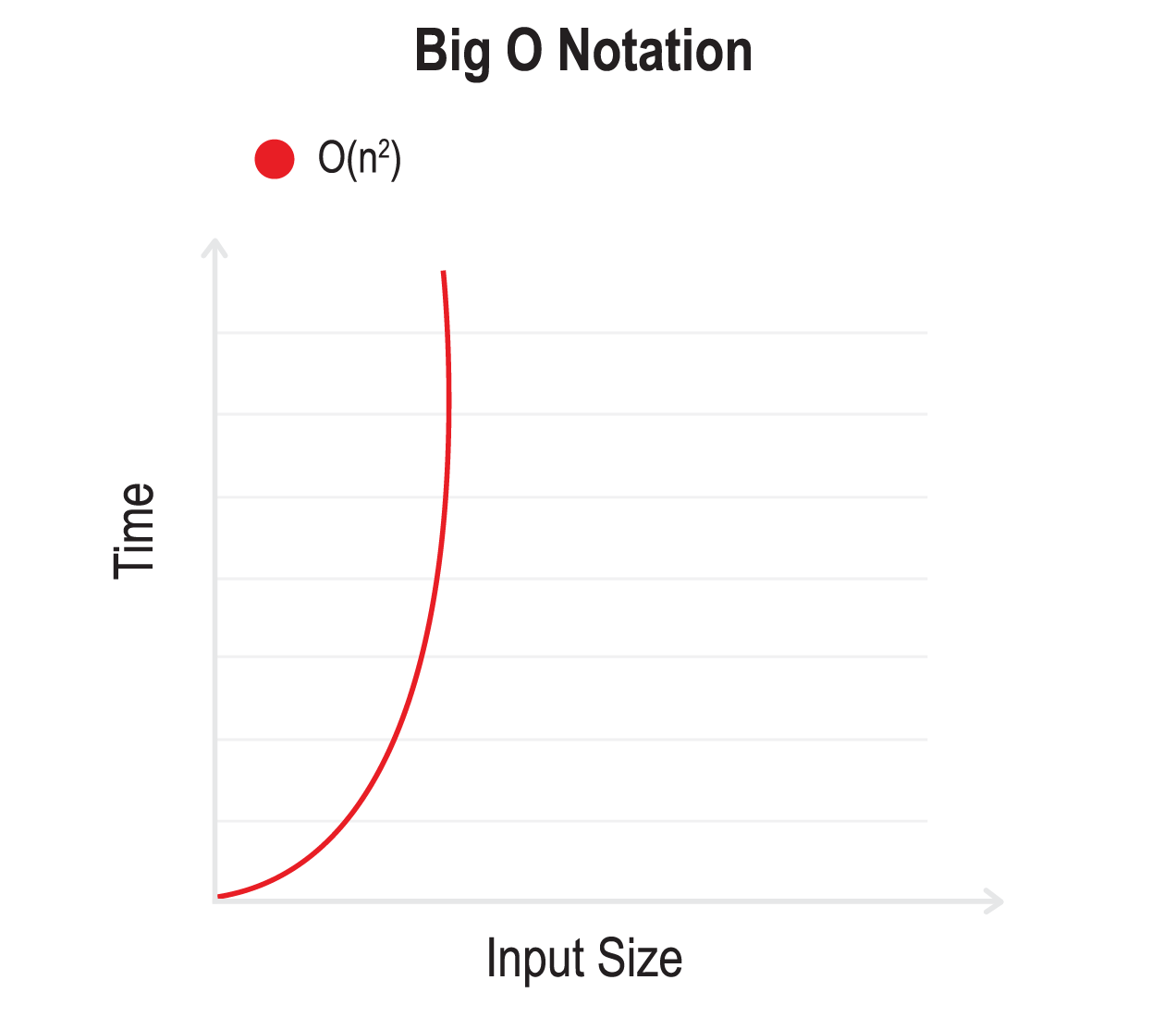
O(n²) - Quadratic time

O(n²) means that the running time is directly proportional to the squared size of the input.

O(n)^2

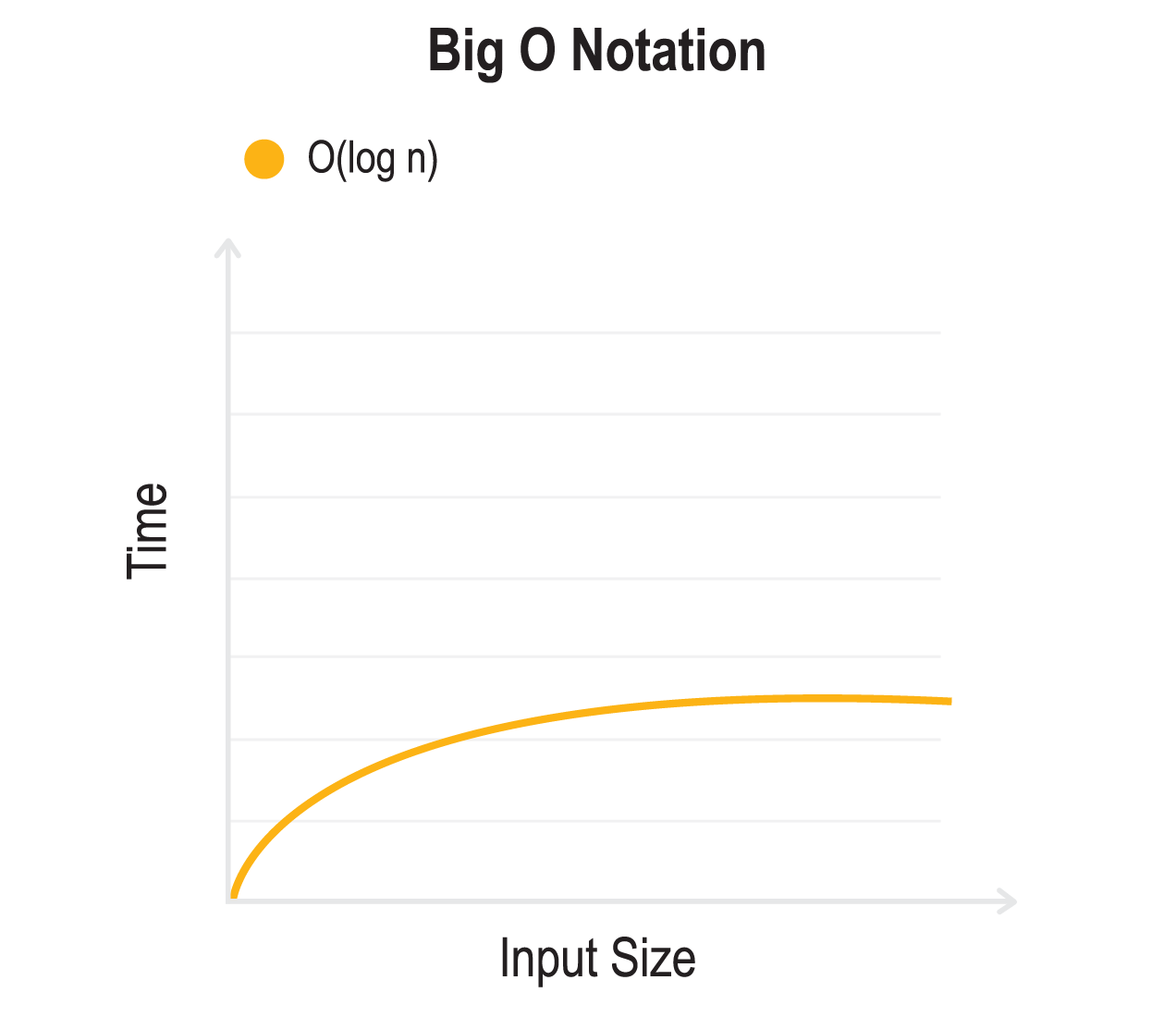
O(log n) - Logarithmic time

O(log n) means that the running time grows proportionally to the logarithm of the input size. The result of this is that the run time barely increases as you exponentially increase the input.

O(log n) Logarithmic Time

Calculating

Calculating time complexity is beyond the scope of this course due to the math and complexity involved. You aren’t required to know how to calculate time complexity at the workplace. Knowing how to do so is typically in data-heavy positions, such as data engineers working on the back end, specifically dealing with large sets of data.

It is, however, still important to keep the Big O time complexities in mind when developing your applications.

If you would like to dive into the mathematics behind the calculations of Big O notation, please look at the links provided in additional resources.

Lesson task

It is highly unlikely you will ever need to calculate Big O notation complexity, but knowing about the different time complexities is important.

Goal

You will be able to explain the differences between the different Big O complexities.

Brief

Complete the Level 1 Process.

NOTE: Lesson tasks do not get submitted on Moodle and are not assessed by tutors. They are mainly there for you to practise what you have learned in the lesson.